Amortized Analysis(분할상환 분석)
18 May 2017평균 러닝타임 분석의 필요성
3 벌의 옷을 산다고 생각해보겠습니다. 각각의 옷은 1만 원, 2만 원, 3만 원입니다. 이 때 옷을 사는데 필요한 금액은 6만 원입니다. 자 그런데 우리가 아는 정보가 “옷 한 벌당 최대 3만원” 밖에 없다면 우리가 준비해야 하는 비용은 어떻게 되나요? 3벌의 옷을 구매하고 옷은 항상 3벌을 사야하기 때문에 최악의 상황을 대비하여 총 9만 원이 필요합니다. “옷 한 벌당 최대 3만원” 의 정보만 으로는 불필요한 3만 원을 더 준비해야 합니다.
자, 그런데 여기에 옷 한 개 구매 당 평균 비용이 2만 원 이라는 정보를 추가적으로 알게 된다면 우리가 준비해야 하는 돈은 어떻게 될까요? 네, 정확히 6만 원만 준비하면 됩니다. 이 때 필요한 돈 6만원이 어떻게 사용되는지 조금 자세히 살펴보면 다음과 같습니다.
- 평균비용을 통해 각각의 옷마다 2만 원이 들 것이라 예상하고 6만 원을 준비합니다.
- 구매하는 옷이 2만 원이라면 그대로 2만 원을 사용합니다.
- 옷이 2만 원보다 비싸다면, 부족한 금액을 2만 원보다 싼 옷에서 보충합니다.
너무 당연한 얘기를 장황하게 써놓았다고 생각할 수 있습니다만, 이것이 분할상환분석의 핵심입니다.
분할상환분석은 알고리즘의 러닝타임을 분석하는 방식중 하나입니다. 기존에 우리는 알고리즘 러닝타임 분석을 코드 라인들의 Big-O 를 통해 표현하였습니다. 그리고 Big-O 는 항상 최악을 가정하기 때문에 전체 알고리즘 비용을 어떤 경우에 실제 최악의 경우가 거의 발생하지 않음에도 불구하고, 최악으로 잡습니다. 이 때 분할상환분석은 전체비용의 평균이라는 추가적인 정보를 제공하여 실제 연산의 비용 판단에 도움을 줍니다.
이진수를 1씩 증가시키는 이진 카운터(Binary Incrementer)를 예로 들어보겠습니다.
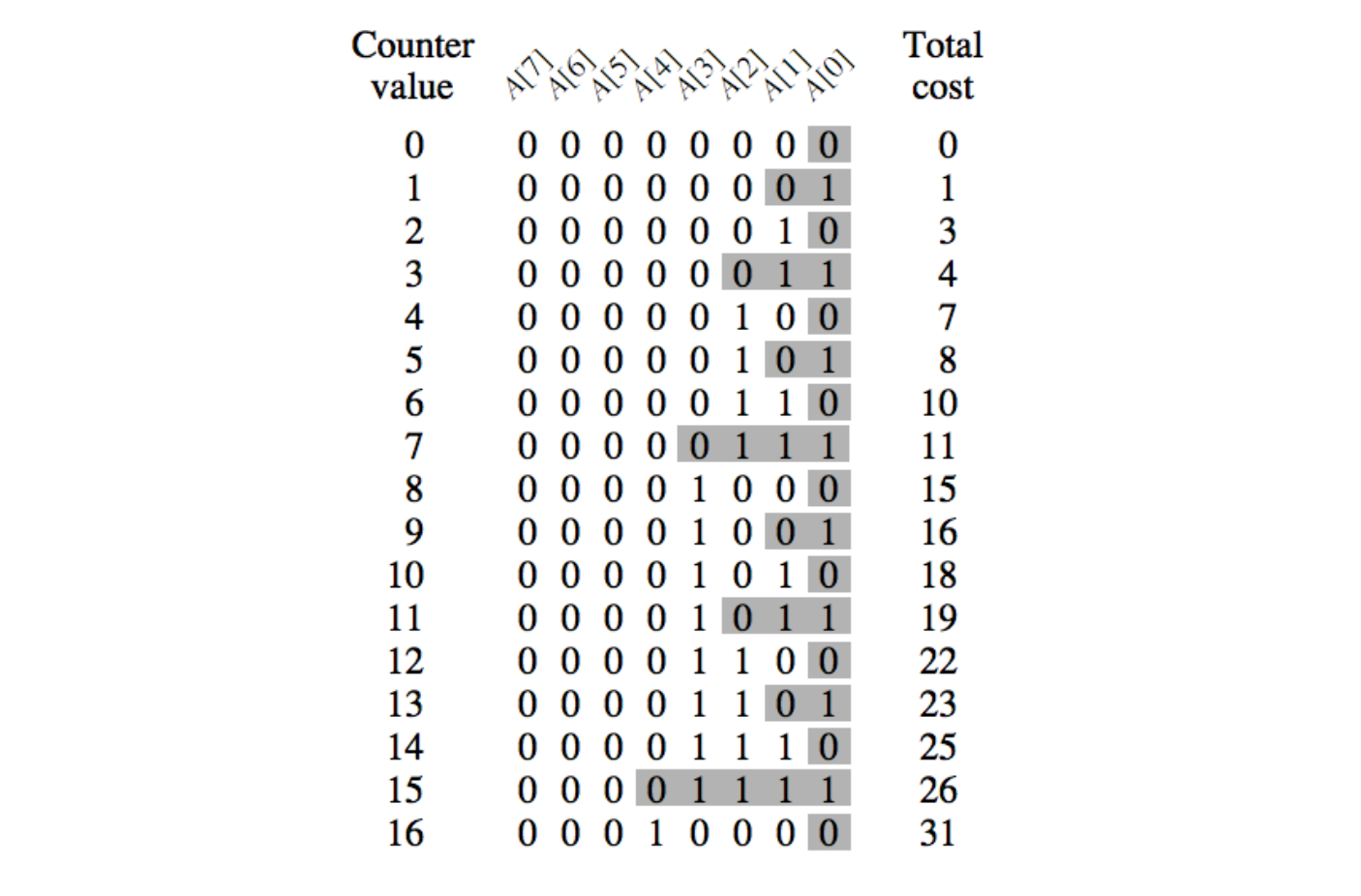
이진 카운터는 일정한 길이의 배열에 0과 1을 저장하여 이진수를 표현하는 데이터를 1씩 증가시키는 함수입니다. 자 그런데 위의 그림에서 보듯이, 이진수를 1씩 증가 시킬 때 반전되는 값의 개수(비용)는 매 반복마다 일정하지가 않습니다. 예를 들어 15(10)인 수를 16으로 만들 경우 01111(2)를 10000(2)로 만들 때 5개의 값을 반전시킵니다. 그렇지만 16에서 17로 증가할 때는 10000(2)가 10001(2)되는 것이므로 1개의 값만 반전됩니다. 즉, 4개의 반전 작업이 절약되는 것입니다. 이 반전이라는 비용은 일정하게 증가하는 것이 아니라, 매 log2n(log 베이스 2) 값이 자연수가 될 때마다 목표치에 도달하는 형태를 취하고 있는 것입니다.
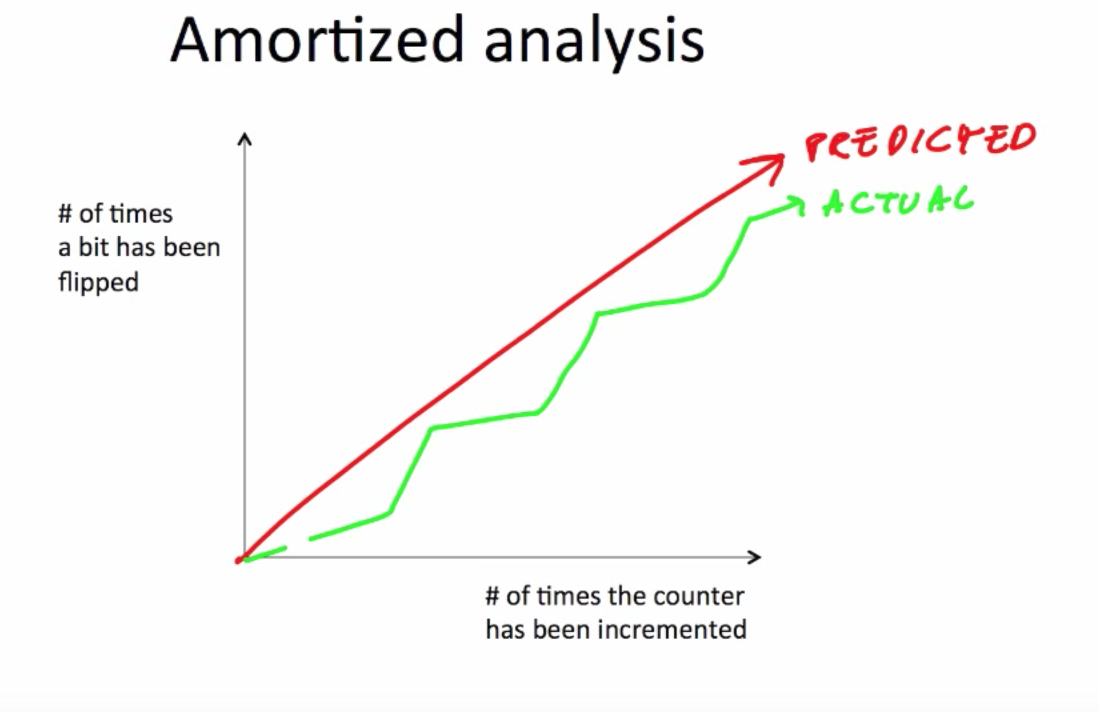
여기서 분할상환 분석의 필요성이 나타납니다. 일반적으로 비용 분석은 최악의 경우를 비용으로 잡고 분석합니다. 하지만, 때때로 최악의 경우를 비용으로 잡는 것이 위처럼 매 연산에 비용을 과하게 부과하는 상황이 발생합니다. 그렇기 때문에 전체 연산의 과정이 평균적으로 어느 정도의 비용이 필요한지를 구하는 것이 연산을 합리적으로 바라보는 시각에 도움을 줄 수 있습니다.
CLRS에서 소개하는 분석 방식은 크게 총계분석, 결산방법, 잠재비용방법이 있습니다. 각각의 분석이 어떤 방식으로 이뤄지는지 하나씩 살펴보겠습니다.
1. 총계분석(Aggregate method)
무슨 의미인지 Stack을 예로 설명하겠습니다. Stack에는 기본적으로 push, pop의 메소드가 있습니다. 이 때 각각의 연산의 비용을 1이라고 정했을 때 시간복잡도는 어떻게 될까요? 네, 둘 모두 O(1)입니다. 왜냐하면 push, pop은 둘 다 top을 기준으로 원소를 넣고 빼는 위치가 정해져 있기 때문입니다. 이 때 n개 연산에 대한 push, pop 각각의 시퀀스 비용은 어떻게 될까요? 여기서 n개 연산의 시퀀스 비용이라는 것은 해당 연산을 n번 할 경우 발생하는 총 비용에 시간복잡도를 곱한 것을 의미합니다. 즉, push의 비용은 1이고 시간복잡도는 O(1)이므로 연산이 n번 일어났을 때 push 연산의 시퀀스 비용은 O(n)입니다.(pop도 O(n)입니다.)
| 비용 | 시간 복잡도 | n번 수행 시퀀스 비용 | |
|---|---|---|---|
| Push | 1 | O(1) | O(n) |
| Pop | 1 | O(1) | O(n) |
총계분석에서는 n번 수행한 각각의 시퀀스 비용을 합산(T(n))하여 이를 n으로 나눈 값을 분할상환비용(Amortized Cost) 이라고 말합니다. 이 비용은 O(n)/n이므로 O(1)이 됩니다.
그럼 여기서 해당 스택에 MultiPop이라는 연산을 추가해보겠습니다. 그렇다면, 분할상환비용은 변할까요? 그럴수도 있고 아닐 수도 있습니다. 총계분석은 자료구조 내의 모든 연산의 시퀀스 비용을 합산합니다. 그렇기 때문에 연산을 추가한다는 것은 평균을 내기 위한 값을 하나 더 추가한다는 것을 의미합니다. 그렇기 떄문에 위의 경우에서 MultiPop을 추가한다는 것은 다시 말해서 MultiPop의 n번 수행한 시퀀스 비용을 합산값에 추가해야 합니다. 그래서 이 때 그 값이 O(n)이라면 분할상환비용은 여전히 O(1)일 것이고, 그렇지 않다면 값이 변해야 합니다.
여기서 문제가 되는 것은 MultiPop의 n번 수행한 시퀀스 비용입니다. 이를 코드 기반으로 생각해서 MultiPop은 Pop이 n번 수행되는 것이기 때문에 비용이 n, 시간 복잡도가 O(n)이므로, n번 수행한 시퀀스 비용이 O(n^2)이라고 분석할 수도 있습니다. 이는 맞는 분석입니다만 이 비용을 모든 경우에 만족하면서 더 낮게 설정할 수 있습니다. 그리고 핵심 아이디어는 Pop은 Push된 횟수만큼만 일어난다 입니다. 즉, Push가 n번 일어나면 MultiPop은 n번 이상으로 일어날 수 없다는 것입니다. 그 결과 MultiPop의 n번 수행한 시퀀스 비용은 O(n)이 됩니다.
| n번 수행 시퀀스 비용 | |
|---|---|
| Push | O(n) |
| Pop | O(n) |
| MultiPop | O(n) |
그렇기 때문에 MultiPop연산을 추가해도 해당 스택의 분할상환비용은 O(3n)/n으로 O(1)이 됩니다.
그렇다면 여기다가 MultiPush연산이 추가되면 어떻게 될까요? 여기서 고민해야 되는 것은 최악의 경우 입니다. MultiPush가 추가되기 전에는 Push가 n번 일어나는 것이 최악의 비용을 만들어내지만, MultiPush가 있는 경우에는 MultiPush가 n번 일어나는 것이 최악의 경우가 됩니다. MultiPush는 Push가 n번 일어나기 때문에 비용이 n이고, 시간복잡도는 O(n)이 되어 n번 수행한 시퀀스 비용은 O(n^2)이 됩니다. 그러므로 이 때 분할상환 비용은 O(n)이 됩니다.
참고자료
- Introduction to Algorithms 3rd Edition, Ch 17
- Amortized Analysis - Youtube